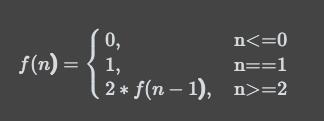斐波那契数列

发表于

  • 题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法

第一种方法

1
2
3
4
5
6
7
8
9
10
function  cal(n){
    if(n<=0){
        return -1;
    }
    if(n==1||n==2){
        return n;
    }else{
        return cal(n-1)+cal(n-2);
    }
}

第二种方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function JumpFloor(n){
if(n<0){
    return 0
}
var fibArry = [0,1,2]
if(n<3){
  return fibArry[n]
}
var nReturn;
var fibFirst=1,fibTow=2;
for (var i = 3; i <= n; i++)             
  {
      nReturn =fibFirst + fibTow;                 
      fibFirst=fibTow ;
      fibTow = nReturn;
  }            
  return nReturn;
}

  • 题目描述

    一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

假设f(n)是n个台阶跳的次数。

解析：

  1. f(1) = 1

  2. f(2) 会有两个跳得方式，一次1阶或者2阶，这回归到了问题f(1),f(2) = f(2-1) + f(2-2)

  3. f(3) 会有三种跳得方式，1阶、2阶、3阶，那么就是第一次跳出1阶后面剩下：f(3-1);第一次跳出2阶，剩下f(3-2)；第一次3阶，那么剩下f(3-3).因此结论是
    f(3) = f(3-1)+f(3-2)+f(3-3)

  4. f(n)时，会有n中跳的方式，1阶、2阶…n阶，得出结论：

f(n) = f(n-1)+f(n-2)+…+f(n-(n-1)) + f(n-n) => f(0) + f(1) + f(2) + f(3) + … + f(n-1) == f(n) = 2*f(n-1)

所以，可以得出结论

java实现

1
2
3
4
5
6
7
8
9
10
11
12
public class Solution {
    public int JumpFloorII(int target) {
        if(target==0){
            return 0;
        }
        if(target==1){
            return 1;
        }
        return 2*JumpFloorII(target-1);
    }
}

javascript实现

1
2
3
4
5
6
7
function JumpFloorII(n){
    if(n==0)
        return 0;
    if(n==1)
        return 1;
    return 2*JumpFloorII(n-1);
}

  • 题目描述

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

解析：斐波那契数列

  1. f（1）=1
  2. f（2）=2
  3. f(n)=f(n-1)+f(n-2)

java实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
    public int RectCover(int target) {
        if(target==0){
            return 0;
        }
        if (target == 1) {
            return 1;
        }
        if (target == 2) {
            return 2;
        }
        return RectCover(target - 1) + RectCover(target - 2);
    }
}

javascript实现

第一种方式：递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function RectCover(n){
    if(n==0){
        return 0;
    }
    if(n==1){
        return 1;
    }
    if(n==2){
        return 2;
    }
    return RectCover(n-1)+RectCover(n-2);
}

第二种方式：循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function rectCover(n)
{
    if(n==0||n==1||n==2){
        return n;
    }
    var nReturn;
    var one = 1,two = 2;
    for(var i=3;i<=n;i++){
        nReturn = one + two;
        one = two;
        two = nReturn;
    }
    return nReturn;
}

关联知识：源码、补码、反码

  • 计算机中的符号数有三种表示方法，即原码、反码和补码。三种表示方法均有符号位和数值位两部分，符号位都是用0表示“正”，用1表示“负”，而数值位，三种表示方法各不相同

  • 特征：

    1
    2
    3
    4
    >       1、一个负整数（或原码）与其补数（或补码）相加，和为模。
    >       2、对一个整数的补码再求补码，等于该整数自身。  
    >       3、补码的正零与负零表示方法相同。
    >

>

  • 求补码：(a) 正数的补码与源码相同 . （b） 负整数的补码，将其对应正数二进制表示所有位取反（包括符号位，0变1，1变0）后加1

  • 题目描述

输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

解析：利用位运算来实现 思路： 将n与n-1做与运算，会把最右边的1去掉。 比如： 1100 & 1011 = 1000 ，即 12 & 11 = 8

再利用计算器count++计算出有多少个 1 即可

1
2
3
4
5
6
7
8
9
function NumberOf1(n)
{
     var count = 0;
     while (n != 0) {
          count++;
          n = n & (n - 1);
     }
     return count;
}

n&(n-1)妙用

  • 求某一个数的二进制表示中1的个数 
1
2
3
4
5
6
7
>    while (n >0 ) {
>
>        count ++;
>
>        n &= (n-1);
>    }
>

>

  • 判断一个数是否是2的方幂：n > 0 && ((n & (n - 1)) == 0 )

  • 计算N!的质因数2的个数：
    容易得出N!质因数2的个数 = [N / 2] + [N / 4] + [N / 8] + ….

    下面通过一个简单的例子来推导一下过程：N = 10101(二进制表示）

    现在我们跟踪最高位的1，不考虑其他位假定为0，

    则在

    [N / 2] 01000

    [N / 4] 00100

    [N / 8] 00010

    [N / 8] 00001

    则所有相加等于01111 = 10000 - 1

    由此推及其他位可得：(10101)!的质因数2的个数为10000 - 1 + 00100 - 1 + 00001 - 1 = 10101 - 3(二进制表示中1的个数)

    推及一般N!的质因数2的个数为N - （N二进制表示中1的个数）